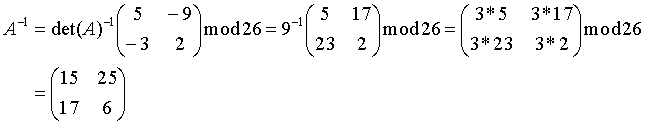Cryptography
What is cryptography?
- Formal Definition: The art or science concerning the principles, means, and methods for rendering plain information unintelligible, and for restoring encrypted information to intelligible form. (National Information Systems Security (INFOSEC) Glossary, 1999)
- Informal: The basic objective of cryptography is to enable two people, whom are usually referred to as Alice and Bob in the text that I read, to communicate over an insecure channel in such a way that an opponent, usually referred to as Oscar, cannot understand what is being said. This channel could be a telephone line or computer network, for example.
Image is missing in html document.
Basic Terminology.
- The information that Alice sends to Bob, which is called plaintext, can be English text, numerical data, zeros and ones, or anything at all – its structure is completely arbitrary.
- Alice encrypts the plaintext, using a predetermined key, and sends the resulting ciphertext over the channel.
- Oscar, upon seeing the ciphertext in the channel by eavesdropping, cannot determine what the plaintext was.
- But Bob, who knows the key, can decrypt the ciphertext and reconstruct the plaintext.
This concept leads us to the following definition.
Definition
- A cryptosystem is a five-tuple (P, C, K, E, D), where the following conditions are satisfied:
- P is a finite set of possible plaintexts.
- C is a finite set of possible ciphertexts.
- K, the keyspace, is a finite set of possible keys.
- For each kÎ K, there is an encryption rule ekÎ E and a corresponding decryption rule dkÎ D. Each ek: P® C and dk: C® P are functions such that dk(ek(x)) = x for all plaintext xÎ P.
The main property is property 4. It says that if a plaintext x is encrypted using ek, and the resulting ciphertext is subsequently decrypted using dk, then the original plaintext x results. Clearly, ek is one-to-one, otherwise, decryption could not be accomplished in an unambiguous manner. For example, if y = ek(x1) = ek(x2) where x1 ¹ x2, then Bob has no way of knowing whether y should decrypt to x1 or x2.
Two Types of Cryptosystems
- Cryptosystems can be broadly classified into symmetric-key systems and public-key systems.
- A public-key system uses two keys, a public key to encrypt the messages and a private key to decrypt them.
- (say how we will discuss much more about these tomorrow)
- A symmetric-key system, or secret-key system, in contrast is a cryptosystem in which the sender and the receiver of a message, share a single common key that is used to encrypt and decrypt messages.
- (this is what we will talk about today)
For today, we will be assuming that Alice and Bob have chosen a random key and exchanged secretly either in person or over a secure line. Now lets get to some simple cryptosystems. I will go through this first basic cryptosystem in excrutiating depth in order to really give a feel for what is going on.
Shift Cipher
- The idea behind shift cipher is based on closure and inverses of addition in the group Zm, where m is a positive integer.
- We will use shift cipher to encrypt ordinary English text by setting up a correspondence between alphabetic characters and residues modulo 26 as follows A« 0, B« 1, …, Z« 25.
- Shift Cipher is defined by P = C = K = Z26. For 0 £ k £ 25, define
ek(x) = (x + k) (modulo 26)
and
dk(y) = (y – k) (modulo 26)
for all x,yÎ Z26.
Is This a Cryptosystem?
- Properties 1, 2, and 3 are clearly met, i.e., the set of plaintexts, the set of ciphertexts, and the keyspace all are finite.
- We must check property 4.
- Let kÎ K and xÎ P, arbitrary.
- dk(ek(x)) = dk((x + k)(mod 26)) = ((x + k) – k) (mod 26) = x (mod 26) = x.
- Therefore, Shift Cipher is in fact a cryptosystem.
Here’s a simple example of the shift cipher in action. We will refer to the correspondences below for the example.
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
|
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
Example
- Suppose the key is k = 11, and the plaintext to be sent is
marinersarethebest
- We first convert the plaintext to a sequence of integers using the above correspondence, obtaining the following:
|
12 |
0 |
17 |
8 |
13 |
4 |
17 |
18 |
0 |
|
17 |
4 |
19 |
7 |
4 |
1 |
4 |
18 |
19 |
- Next, we add 11 to each value modulo 26 to yield:
|
23 |
11 |
2 |
19 |
24 |
15 |
2 |
3 |
11 |
|
2 |
15 |
4 |
18 |
15 |
12 |
15 |
3 |
4 |
- Finally, we convert the sequence of integers to alphabetic characters, obtaining the ciphertext:
XLCTYPCDLCPESPMPDE
- This is the message that is sent. To decrypt the ciphertext, Bob will first convert the ciphertext to a sequence of integers, then subtract 11 from each value (mod 26), and finally convert the sequence of integers to alphabetic characters.
I’m sure that all of us have seen puzzles like this in the newspaper or puzzle books and realize that this is not a difficult system to break. Just trying all the keys, although cumbersome, would not be difficult in the Shift Cipher, that is one of the reasons, in practice, it is not secure. The process of attempting to compute the key k, given a string of ciphertext, is called cryptanalysis. In general, we want cryptosystems in which an exhaustive key search is impossible(even for computers).
Now lets study a cryptosystem that has more algebra involved and a larger keyspace.
Affine Cipher
- In the affine cipher, we restrict our encryption function to functions of the form:
e(x) = (ax + b)(mod 26), where a,bÎ Z26, a ¹ 0.
- These functions are called affine functions, hence the name.
- In order that decryption is possible, it is necessary to ask when an affine function is one-to-one. In other words, for any yÎ Z26, we want the congruence
ax + b º y (mod 26) to have a unique solution for x.
- This congruence is equivalent to ax º (y – b) (mod 26)
- Now, as y varies over Z26, so, too, does y – b vary over Z26. Hence, it suffices to study the congruence ax º y (mod 26), for yÎ Z26, i.e., if this congruence holds for all yÎ Z26, then it will also hold for all y – b, if bÎ Z26, because y – bÎ Z26.
Nonexample: 2x º 0 (mod 26). This has two solution, x = 0 and x = 13, for the particular y = 0 and thus a = 2 will not work for a one-to-one affine function.
Trying out some elements of Z26, we start to discover that only some values of a have this property.
Claim: This congruence has a unique solution for every y if and only if gcd(a,26) = 1.
Proof
- ‘Þ ’ Suppose the congruence has a unique solution for every y.
- (RAA) Assume gcd(a,26) ¹ 1.
Note: a can be 0 because 0x º 0 (mod 26), has 26 solutions.
- Then gcd(a,26) = d > 1.
- Thus the congruence ax º 0 (mod 26) has at least two distinct solutions, namely x = 0 and x = 26/d, for the particular y = 0. x = 0 works obviously. Because d | a and d | 26, therefore, $ m,nÎ Z26 such that dm = a and dn = 26.
So 26/d = n. And an = (dm)n = (dn)m = 26m º 0 (mod 26).
This is a contradiction.
- Therefore, gcd(a,26) = 1.
- ‘Ü ’ Suppose gcd(a,26) = 1.
- Assume x1, x2Î Z26, such that ax1 º ax2 (mod 26)
- Then a(x1 – x2) º 0 (mod 26)
- Thus, 26 | a(x1 – x2).
- By Lemma (*), or simply by division property, since 26 | a(x1 – x2), and gcd(a,26) = 1, we must therefore have that 26 | (x1 – x2).
i.e. x1 º x2 (mod 26) and the congruence has a unique solution.
For example, since gcd(4,26) = 2, it follows that ek(x) = 4x + 7 is not a valid encryption function: x and x + 13 will encrypt to the same value, for any xÎ Z26. Specifically,
ek(a) = ek(0) = 4(0) + 7 (mod 26) = 7, and ek(n) = ek(13) = 4(13) + 7 (mod 26) = 7.
Lemma(*): If a,b,cÎ Z26 such that gcd(a,b) = 1 and a | bc, then a | c.
Proof
- a | bc Þ $ nÎ Z26 such that an º bc (mod 26).
- gcd(a,b) = 1 Þ $ r,sÎ Z26 such that ar + bs º 1 (mod 26).
(the gcd is a linear combination)
- (arc + bcs) º c (mod 26) (multiplying by c, distributing, associativity of ring)
- arc + ans º c (mod 26) (substitute an for bc)
- a(rc + ns) º c (mod 26) (distribution in Z26)
- rc + ns (mod 26)Î Z26, thus a | c.
Note: There is nothing special about 26, this result can be generalized for any positive integer m > 1.
Thm. The congruence ax º b (mod m) has a unique solution xÎ Zm if and only if gcd(a,m) = 1.
So we have shown that the only one-to-one affine functions in Z26 are those of the form ax + b (mod m) where gcd(a,m) = 1 and bÎ Z26.
We have shown that the Affine Cipher satisfies the first 3 properties of the definition of a cryptosystem and that it satisfies the need for a one-to-one encryption rule, but we still need an associate decryption rule in order to decrypt the ciphertext.
The Decryption Rule
- Consider our congruence y º ax + b (mod 26). This is equivalent to
ax º y – b (mod 26).
We would like to say that x º a-1(y – b) (mod 26), but not all aÎ Z26 have an inverse.
- It turns out that the a values which have a multiplicative inverse modulo 26 are exactly those which satisfy gcd(a,26) = 1.
(ask if you want to be shown, Lemma (*2))
- Since in encryption the a always satisfies this condition.
- Thus, x º a-1(y – b) (mod 26), which is the form of the decryption function
Lemma(*2): Let a and n be integers, with n > 1. Then a has a multiplicative inverse modulo n if and only if gcd(a,n) = 1.
Proof
- ‘Þ ’ First, suppose that a has an inverse modulo n.
- Then there is a k such that ak º 1 (mod n).
- Thus, n is a divisor of ak – 1, so there must be some integer t so that
ak – 1 º nt (mod n).
- Rewriting this as ak – nt º 1(mod n), we see that gcd(a,n) = 1.
- ‘Ü ’ Now, suppose that gcd(a,n) = 1. Then there are integers r and s with
ar + ns = 1.
- This means ar – 1 is divisible by n.
- So ar º 1 (mod n).
- This tells us r is the inverse of a.
Putting this all together, we finally obtain our Affine Cipher.
Affine Cipher Overview
- The Affine Cipher is defined by P = C = Z26 and let
K = {(a,b)Î Z26xZ26 : gcd(a,26) = 1}
For k = (a,b)Î K, define
ek(x) = (ax + b) (mod 26)
and dk(y) = a-1(y – b) (mod 26), for all x,yÎ Z26.
- We must check property 4.
- Let k = (a,b)Î K and xÎ P, arbitrary.
- dk(ek(x)) = dk((ax + b)(mod 26)) = a-1((ax + b) – b) (mod 26)
= a-1(ax) (mod 26) = x (mod 26).
- Therefore, the affine cipher is indeed a cryptosystem.
Example:
- We want to send the word, dog, using the key k = (3,5), gcd(3,26) = 1, so this key is okay.
- We get the corresponding integers as before: 3, 14, 6.
- Then we multiply by 3 and add 5 modulo 26 to yield: 14, 21, 23, so the message is: OVX.
- 3-1 = 9, so to decrypt we take the ciphertext corresponding integers and subtract 5 then multiply by 9 modulo 26 to get back to: 3, 14, 6.
Note: We have developed the set {aÎ Zm : gcd(a,m) = 1}. We will denote this set as Zm*. We have introduced that Zm* has inverses, identities, associativity, and commutativity. It turns out that Zm* is in fact an abelian group called the prime residue group.
Proof of closure:
Let x, yÎ Zm*. Then gcd(x,m) = 1 and gcd(y,m) = 1. Then for some r,s,t,uÎ Z,
xr + ms º 1 (mod m) and yt + mu º 1 (mod m). Multiplying together yields,
(xr + ms)(yt + mu) º 1 (mod m)
xy(rt) + xrmu + ytms + mmsu º 1 (mod m),
or xy(rt) + m(xru + yts + msu) = 1 (mod m), rtÎ Z, and xru + yts + msuÎ Z.
Therefore, gcd(xy,m) = 1. Closure.
Do We Have a Larger Keyspace?
- First a definition, the number of integers in Zm that are relatively prime to m is often denoted by f (m)(this function is called the Euler phi-function).
- In the Affine Cipher, the number of choices for b is m, and the number of choices for a is f (m). Thus, the number of keys in the keyspace for the Affine Cipher over Zm is mf (m).
- In the special case where m = 26, f (26) = 12 (1,3,5,7,9,11,15,17,19,21,23,and 25 are all relatively prime to 26), so the size of the keyspace = 26(12) = 312, which is larger, but not secure by any means.
Note: In both the Shift Cipher and the Affine Cipher, once a key is chosen, each alphabetic character is mapped to a unique alphabetic character. For this reason, these cryptosystems are called monoalphabetic. These type of systems are easy to break by simply looking for the most common letters in the ciphertext and trying out the most common English letters in their place until an intelligible message is formed.
The following cryptosystem corrects these faults by offering a polyalphabetic approach to encryption.
Vigenere Cipher
- The Vigenere Cipher was invented in the sixteenth century, and is associated with the idea of adding a keyword of length m to the plaintext that is to be sent.
- This cipher encrypts m alphabetic characters at a time.
- The Vigenere Cipher is defined by P = C = K = (Z26)m.
For a key k = (k1, k2,…, km), we define
ek(x1, x2, …, xm) = (x1 + k1, x2 + k2, …, xm + km)
and dk(y1, y2, …, ym) = (y1 – k1, y2 – k2, …, ym – km), all operations in Z26.
- Verifications that this is a cryptosystem is left to the reader.
Example:
- Suppose m = 7 and the keyword is ENCRYPT. This corresponds to the numerical key k = (4, 13, 2, 17, 24, 15, 19). And suppose the plaintext is:
thissystemsecure
- We convert to plaintext and add the key modulo 26, as follows:
|
19 |
7 |
8 |
18 |
18 |
24 |
18 |
19 |
4 |
12 |
18 |
4 |
2 |
20 |
17 |
4 |
|
4 |
13 |
2 |
17 |
24 |
15 |
19 |
4 |
13 |
2 |
17 |
24 |
15 |
19 |
4 |
13 |
|
23 |
20 |
10 |
9 |
16 |
13 |
11 |
23 |
17 |
14 |
9 |
2 |
17 |
13 |
21 |
17 |
- This turns into the ciphertext: XUKJQNLXROJCRNVR
- Decryption is done in the same manner, just subtracting the keyword instead of adding.
Larger Keyspace
- The Vigenere Cipher has a keyspace of 26m, for a keyword of length m.
- For our example the keyspace is 267 = 8031810176.
- This makes it a lot more difficult to do an exhaustive key search.
- Unfortunately, there are other forms of cryptanalysis and the Vigenere Cipher becomes susceptible to many types if the ciphertext is long.
Let’s build another polyalphabetic cryptosystem this time using some linear algebra.
The Hill Cipher
- The strategy behind the Hill Cipher is to take m linear combinations of the m alphabetic characters a plaintext, producing m alphabetic characters in a ciphertext.
- The idea is that if we have a plaintext string of length m, (x1, x2, …, xm)
and m linear combinations: k11x1 + k12x2 + … + k1mxm
k21x1 + k22x2 + … + k2mxm
…
km1x1 + km2x2 + … + kmmxm
Then we can get (y1, y2, …, ym) by:
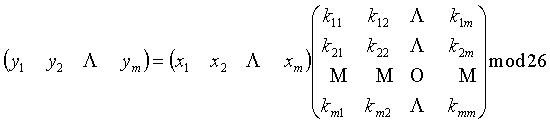 , where kijÎ Z26.
, where kijÎ Z26.
Decryption of the Hill Cipher
- This system seems fine until we consider decryption.
- In order, to retrieve the plaintext from a ciphertext we are going to need the inverse of the encryption matrix, i.e., if y = Ax, then we want to find A-1 such that x = A-1y.
- If all the entries are in a field then we know that the invertible matrices are exactly the ones in the general linear group, however, Z26 is not a field, so what do we do.
- From linear algebra, we know that a real matrix K has an inverse if and only if its determinant is non-zero. We need to find some sort of analygous idea in Z26.
Claim: A matrix K has an inverse modulo 26 if and only if gcd(det K, 26) = 1.
Proof
- ‘Þ ’ First, suppose that gcd(det K, 26) = 1.
- Then the det K has an inverse in Z26. (We proved this earlier)
- Now, for 1 £ i £ m, 1 £ j £ m, define Kij to be the matrix obtained from K by deleting the ith row and the jth column.
- Define a matrix K* to have as its (i,j)-entry the value (-1)i+jdet Kji.
- Then it can be shown that K-1 = (det K)-1K*. (skipping over stuff here)
- Hence, K has an inverse.
- ‘Ü ’ Now, suppose that K has an inverse, K-1.
- 1 = det I = det (KK-1) = det K det K-1
- Thus, det K is invertible in Z26.
- Therefore, gcd(det K, 26) = 1.
Hill Cipher Overview
- The Hill Cipher is defined by, for some fixed positive integer m, P = C = (Z26)m, and let K = { A : A is an m x m matrix and gcd(det A, 26) = 1}
For a key A, we define
eA(x) = Ax (mod 26)
and dA(y) = A-1y (mod 26), for all x,yÎ Z26.
- Verifications that this is a cryptosystem is left to the reader.
Example:
- Let m = 2 and take
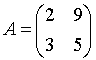 , to encrypt the plaintext: hello
, to encrypt the plaintext: hello
- First we break up the word into pairs, adding a dummy character, say ‘r’ in the case of an odd number of characters. This yields: he ll or.
- Converting to integers we get: (7 4) (11 11) (14 17)
- A(7 4) mod 26 = (0 5), A(11 11) mod 26 = (3 24), A(14 17) mod 26 = (1 3)
- The associated ciphertext is: AFDYBD
- det A mod 26 = -17 mod 26 = 9, gcd(9, 26) = 1, so A has an inverse.
- We can get the inverse by taking the normal inverse in Z and then taking modulus 26.
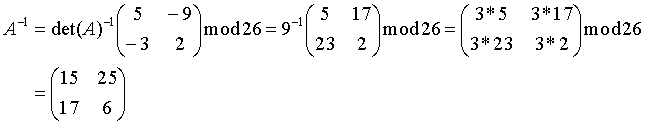
- To recover the plaintext we convert the ciphertext to integer pairs and apply A-1.
- A-1(0 5) mod 26 = (7 4), A-1(3 24) mod 26 = (11 11), A-1(1 3) = (14 17) and we are back to where we started.
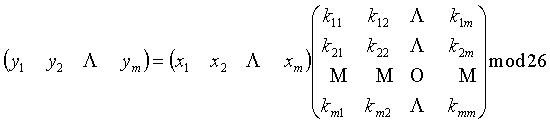 , where kijÎ Z26.
, where kijÎ Z26.  , where kijÎ Z26.
, where kijÎ Z26. 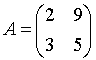 , to encrypt the plaintext: hello
, to encrypt the plaintext: hello